Cómo medían su posición

Si leemos el Derrotero de Francisco Albo, veremos que todos los días en que las condiciones meteorológicas le permiten ver el sol a mediodía toma su altura sobre el horizonte para con este dato determinar su latitud. Vamos a explicar cómo lo hacía tomando por ejemplo esta anotación, que dice así:

28 de abril de 1522. Tomé el Sol en 36º, tenía de declinación 17º, vino a ser la altura 37º escasos.

La latitud es una de las dos coordenadas necesarias para identificar un punto sobre la superficie terrestre. Corresponde a la separación respecto al ecuador, siendo positiva si es al Norte, y negativa si es al Sur, y se mide en grados sexagesimales, es decir, que en el ecuador es cero y en el polo Norte 90º. Cada grado se divide en 60 minutos, y éstos a su vez en 60 segundos.

En el derrotero de Francisco Albo veremos que se refiere a la latitud como apartamiento, altura del polo, o simplemente altura, que en este caso no debería confundirse con la altura medida del sol sobre el horizonte.

Para medir la altura del sol a mediodía sobre el horizonte se utilizaba un instrumento muy sencillo llamado cuadrante, innovador a estas alturas del s. XVI, que consiste básicamente en un arco graduado de 90 grados, de cuyo centro cuelga una plomada. Si apuntamos hacia el sol el lateral del arco en 90 grados, la lectura sobre el hilo de la plomada nos indicará el ángulo de su altura sobre el horizonte.

Cuadrante marino clásico, para medir la altura del Sol sobre el horizonte.

Medir la altura del sol sobre el horizonte no aportaba por sí mismo ningún dato válido sobre la posición que ocupamos en la superficie terrestre, puesto que cada día del año el sol alcanza a mediodía una altura distinta. Para hallar la latitud usando como referencia el sol, o según ellos llamaban, mediante el regimiento del Sol, hay que contar con que desde cualquier punto fijo de la Tierra la altura que alcanza el sol a mediodía es variable a lo largo del año. Esto es debido a la inclinación del eje de rotación terrestre respecto al plano que contiene la órbita terrestre alrededor del Sol, o de la eclíptica.

Por ello, si queremos hallar la latitud nos debemos valer de otro dato, llamado declinación, que es el ángulo comprendido entre el sol de mediodía y el ecuador. Repetimos: entre el sol y el ecuador, no entre el sol y el horizonte como medían los marineros. La declinación del sol es diferente para cada día del año, y oscila entre un ángulo máximo de +23º 45' y mínimo de -23º 45' los días de los solsticios de verano e invierno respectivamente, siendo cero en los equinoccios.

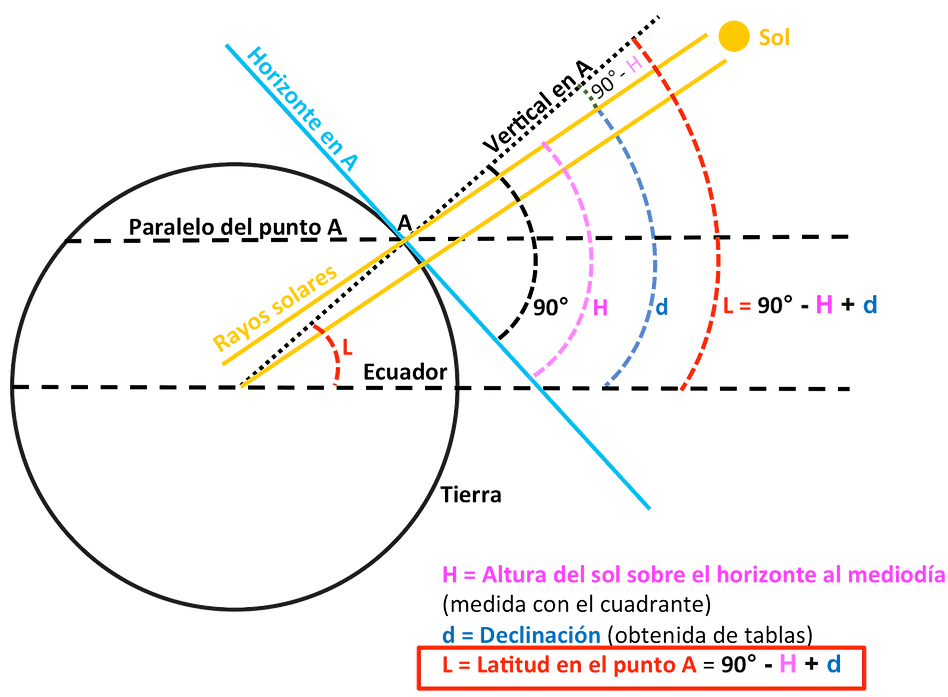
Puesto que la declinación del sol es independiente del lugar de observación y solo depende de la fecha, para obtener la latitud solamente tenemos que medir la altura del sol sobre el horizonte a mediodía, y sumar o restar la declinación correspondiente a la fecha en que nos encontremos. En la práctica, la declinación es un factor de corrección que deberemos aplicar para hallar la latitud, dependiente de la fecha en que nos encontremos, puesto que podemos entenderlo como cuánto de más sube el sol en verano, y cuánto de menos sube el sol en invierno.

Desde el Hemisferio Norte, la declinación deberemos sumarla entre los equinoccios de primavera y otoño, y restarla entre otoño y primavera según la fórmula Latitud = 90º + Declinación - Altura sobre el horizonte. En el Hemisferio Sur se invertirá el signo de la declinación.

Se entiende mejor con un croquis (y doy las gracias a mi amigo Francisco Moreno del Collado por enviarme una versión mejorada del que tenía aquí anteriormente):

Los pilotos portaban la declinación diaria del sol en unas tablas. Por ejemplo, aquí podéis descargar en pdf la Suma de Geographia encargada por el emperador Carlos I a Martín-Fernández de Enciso, "alguacil mayor de la tierra firme de las Indias occidentales" en 1518.

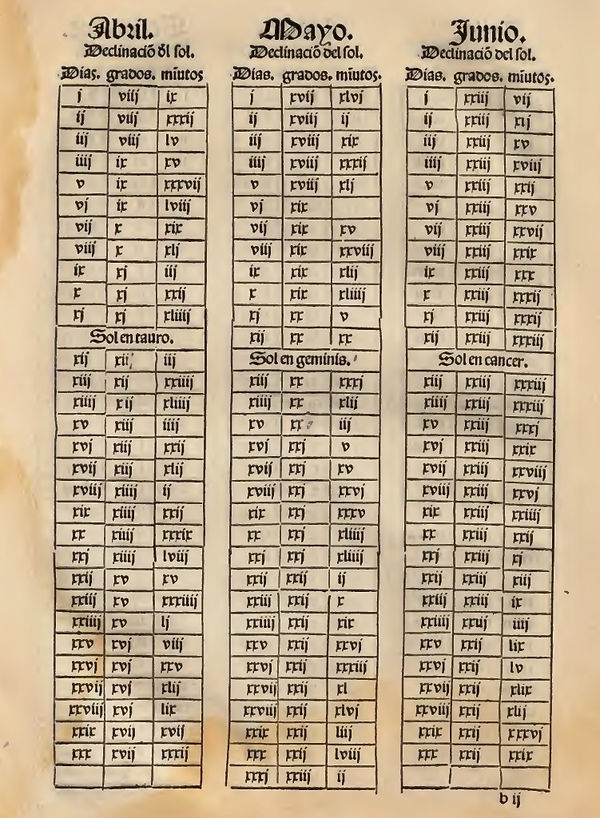
Tabla de declinaciones solares extraída de la obra Suma de Geographia, de Martín-Fernández Enciso, publicada en 1519 -aunque no es la que portaban en la expedición-. Válida para el segundo año después del bisiesto y, por ello, para el año 1522 que estamos usando de ejemplo.

Comprobamos que la declinación correspondiente en la tabla al día que estamos tomando como ejemplo, el 28 de abril de 1522, es de 16º con 59', es decir, que prácticamente coincide con la indicada por Francisco Albo en el Derrotero para este día, que nos decía ser de 17º.

Si desarrollamos la fórmula completa para obtener la latitud de nuestro ejemplo, veremos que coincide exactamente con la determinada por Francisco Albo:

Latitud = 90 + (-17º) - 36º = 37º de latitud Sur.

El signo negativo aplicado al valor de la declinación corresponde al de la fecha, 28 de abril, pero aplicado en el Hemisferio Sur, es decir que en el Hemisferio Norte le correspondería ser positivo, pero al estar navegando en el Hemisferio Sur debe invertirse y quedar como negativo.

Es curioso comprobar cómo por entonces los equinoccios eran el 11 de marzo y el 14 de septiembre. Esto se debe a que hasta el año 1582 estuvo vigente el calendario juliano, que fue sustituído por el gregoriano que seguimos utilizando hoy, y en éste se acumulaba un pequeño error de 11 minutos de más en la duración de cada año. Esto hizo que tras los 1257 años en que estuvo vigente se acumulara un error de 10 días. Por ello, en 1582 después del jueves 4 de octubre de 1582 vino el viernes 15 de octubre.

En el siglo XVI no se conocía todavía ningún método para establecer la otra de las coordenadas, la longitud, que nos indicaría la posición en sentido Este - Oeste, de modo que los marineros la debían estimar con la ayuda del rumbo seguido y la distancia recorrida. El rumbo lo conocían gracias a la brújula, compás o, como ellos llamaban, aguja de marear, mientras que para hallar la distancia recorrida utilizaban la rudimentaria corredera.

Mediante la corredera se podía estimar la velocidad de la embarcación respecto al mar. Para ello hacían falta dos hombres. Uno de ellos lanza al mar por la popa del barco una cuerda con un tronco o una tabla de madera atado en el extremo. La cuerda tiene hechos nudos a intervalos regulares. El otro maneja un reloj de arena. Cuando el tronco se ha estabilizado, el que sujeta la cuerda da una voz avisando de que va a soltarla, y el otro inicia la cuenta del reloj de arena. Mientras se va soltando cuerda al avanzar el barco, se cuentan los nudos hasta que termina el tiempo del reloj de arena. Evidentemente, cuantos más nudos de la cuerda hayan pasado, a mayor velocidad irá el barco, y si conocemos la distancia entre nudos, sabremos también su velocidad. De esta forma se dio origen al término nudo como unidad de velocidad para la navegación.

El problema de esta forma de medir la velocidad es que no tiene en cuenta las corrientes. Si el barco se mueve a favor de la corriente, parecerá que avanza menos de lo que en realidad sí hace. Esto lo sabían perfectamente los navegantes de aquella época, pero no había otra manera de resolver esta cuestión.

No obstante, la corredera como tal no se utilizó hasta algunos años después de este viaje, aunque sí se utilizaban sistemas parecidos que ayudaban a estimar la velocidad.

Corredera y reloj de arena o ampolleta, para medir la velocidad en el mar.

Determinación de la longitud geográfica en la navegación

Mucho se habla de que durante los viajes de descubrimiento y posteriores, desarrollados por españoles y portugueses, se conocía un método para hallar la longitud geográfica, que se mantuvo bajo un escrupuloso secreto, oculto al resto de países competidores.

Lo cierto es que ignoramos si fue así o esto solo es una conjetura. Ningún documento de la época nos describe este hipotético método. Al contrario, las pruebas de que tal método no existía no solo son abundantes, sino siento decir que abrumadoras. De tan secreto que era, nadie sabe nada de él siquiera hoy. Sin embargo, la idea de un supuesto método secreto es tan atractiva, que me temo tendremos que seguir desmintiéndola ad eternum.

El asunto se resolvía a estima, o “por fantasía”, mediante estimaciones diarias de distancias recorridas en el mar, cuya precisión dependía fundamentalmente de la experiencia y de una instrumentación muy rudimentaria, que entre otras cosas no tenía en cuenta el efecto de las corrientes. La maestría marinera de aquellos navegantes y pilotos convertía en suficientes sus estimaciones, de tal manera que a veces resulta tan increíble su acierto que se alimenta la leyenda de que “debían saber algo más de lo que cuentan”. Pero no, simplemente, eran muy buenos en lo que sí conocían.

En el viaje de la primera circunnavegación encontramos un buen ejemplo para desmentir que conocieran un método para hallar la longitud. Durante la travesía del Índico, Elcano va dando estimaciones de distancias pendientes hasta el cabo de Buena Esperanza. Sufre muchos días de tempestades y corrientes contrarias, lo que supone una gran dificultad para conseguir estimaciones veraces. Tanto es así, que cuando por fin cree haber sobrepasado el cabo –lejos de él, sin verlo-, vira al Norte, pero ante su sorpresa se topa con la costa de Sudáfrica más allá de Port Elizabeth, más de 1.000 km al Este de donde creía estar. En este caso no se trataba únicamente de haber hecho estimaciones de distancia recorrida incorrectas. No debemos olvidar que la longitud de las Islas Molucas era ya de por sí algo muy difícil de haber determinado con exactitud, tanto por Elcano como por los portugueses que ya habían estado por allí antes.

Por ello, no solo se trata de una acumulación de errores en las mediciones de distancias recorridas diariamente a lo largo del Océano Índico, sino que incluso el punto de partida, las Molucas, no debía estar localizado en su longitud exacta.

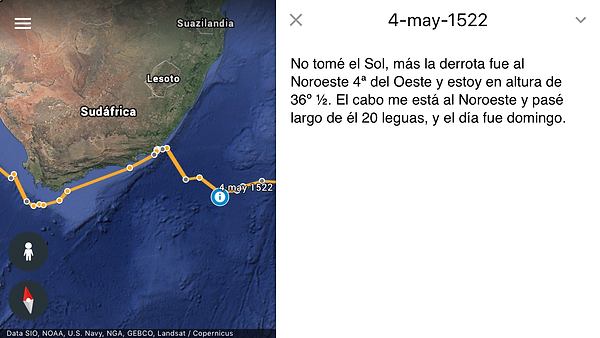
El 4 de mayo de 1522 Elcano cree haber doblado el Cabo de Buena Esperanza, pero en realidad todavía está muy lejos. Al virar al norte, termina topando con la costa sudafricana.

Continuando en descargo del gran Elcano, debemos añadir que durante la travesía del Atlántico hasta España da a menudo estimaciones de distancia a Tenerife que, esta vez sí, resultan muy precisas. Sin duda las hizo con buena mar y viento favorable, ayudado por la Corriente de Benguela, y una vez se había localizado exactamente al pasar cerca del Cabo de Buena Esperanza, cuya longitud ya sí se conocía con mayor aproximación por los múltiples viajes portugueses realizados hasta allí -y por tanto también por nuestros expedicionarios-.

Otro buen ejemplo lo encontramos en el tornaviaje de Urdaneta, desde Filipinas hasta Acapulco. Había un gran interés en ser lo más exacto posible y para ello se contó, además de por el propio Urdaneta, con los pilotos Esteban Rodríguez y Rodrigo Espinosa. Cada uno de ellos hacía sus mediciones y estimaciones. Al final del viaje, había una discrepancia entre ellos de más de 1.000 km en la distancia recorrida para atravesar el Pacífico.

Quien haya leído los derroteros de estos viajes advertirá que nunca se dan longitudes geográficas. Por sí solo éste es otro motivo para negar el supuesto método secreto.

Otro más: el rey Felipe III convocó a principios del s. XVII un concurso de ideas para hallar la longitud. Después lo hicieron Francia, Holanda, e Inglaterra.

El problema de hallar la longitud geográfica a bordo de un navío no fue “oficialmente” resuelto hasta el s. XVIII, cuando el inglés John Harrison inventó un cronómetro lo suficientemente preciso para este fin. Como tantas veces en ciencia, el método teórico estuvo resuelto mucho antes, pero en la práctica no fue posible aplicarlo hasta que se consiguió el avance tecnológico que supuso el cronómetro. Las ampolletas o relojes de arena, y los posteriores relojes que se fueron inventando –p-ej. de péndulo- servían en tierra, pero no en el mar. Dependían de la gravedad, y con el balanceo de un barco esto era un problema. Harrison lo resolvió ingeniosamente, mediante muelles en los mecanismos internos del reloj.

Porque medir la diferencia de longitud geográfica entre dos puntos de la Tierra tomando como referencia los astros implicar medir el tiempo. Si dividimos los 360 grados de la esfera terrestre entre las 24 horas del día, obtenemos que cada hora la Tierra gira 15 grados. Esta es la premisa fundamental para cualquier cálculo.

Por ejemplo: estoy en Sevilla y justo cuando observo que el Sol alcanza su punto más alto en el cielo a mediodía pongo en marcha un cronómetro. Al día siguiente, cuando el Sol alcance nuevamente su punto más alto, podré comprobar cómo han trascurrido 24 horas.

Sin embargo, si me desplazo en dirección Este-Oeste, por ejemplo, a Roma, y me llevo mi cronómetro en marcha, observaré que el Sol alcanza su punto más alto una hora y varios minutos antes que en Sevilla. Así, podemos asegurar que la longitud de Roma respecto a Sevilla es de algo más de 17º.

Hernando Colón, hijo del Almirante Cristóbal Colón, propuso ya en 1524 dotar a las naves de relojes para comparar los tiempos siguiendo este método. Sin embargo, al no haber forma de que los relojes midieran bien, el método fallaba. Por ello se hicieron esfuerzos por hallar otros métodos que facilitaran el asunto:

Alonso de Santa Cruz, en su Libro de las Longitudes, de 1555, describe el Método de los eclipses del sol y de la luna; pero siendo poco frecuentes, difíciles los cálculos, y poco exacto el conocer su principio y su fin, solo le estima útil en las islas y continentes para situarlos bien en las cartas. ”… Que de los lugares do saliesen llevasen bien calculados los eclipses, por hombres doctos en astrología para saber precisamente el día y hora y punto de ella, en que habían allí de comenzar o acabar los tales eclipses, podrían averiguar harto precisamente la longitud de cualesquier lugares, do se pudiesen hallar a los de donde partieron."

Felipe II ordenará en el año 1577 que se hicieran mediciones desde todos los lugares del Imperio aprovechando los dos eclipses de luna que estaban previstos para ese año, ayudando dimensionar así sus territorios.

Galileo descubrirá los 4 satélites principales del planeta Júpiter en 1610. Entonces se descubren sus tránsitos y ocultaciones sobre el disco del planeta, y su observación pronto es utilizada de forma similar al método de los eclipses de sol y de luna, comparando el momento predicho del fenómeno con el momento realmente observado en función del lugar desde el que se hiciera, con la gran ventaja de que en Júpiter estos fenómenos se producen a diario.

Sin embargo, estos métodos no eran viables en la cubierta de un barco, sino que se utilizaban en tierra. Desde un barco es absolutamente imposible mantener Júpiter quieto en el campo de visión de un telescopio de 20 aumentos.

A este método siguió otro que se basaba en la medición de distancias angulares entre la luna y diferentes estrellas. Requería de cálculos complejos, que se fueron simplificando con el uso de tablas astronómicas. De ahí que se desarrollaran los reales observatorios de las diferentes Armadas.

Por todo ello, concluimos que este esfuerzo científico por determinar la longitud geográfica de manera lo más precisa posible fue una carrera de obstáculos, que primero se fue resolviendo con resultados desde tierra firme, y solo hasta la invención del cronómetro pudo ser aplicada con garantías desde las embarcaciones.